Under California’s recently adopted top-two primary system the two candidates who received the highest number of votes in the primary advance to the general election, creating the new phenomenon of general election races between members of the same party. This year, 25 of the 158 legislative and congressional seats will entail intra-party contests. Today, four years after the passage of prop 14, analysts and partisans still debate whether or not Republicans supported the measure at the ballot in 2010. The following analysis attempts to answer that question.
Lauded by those who prefer competitive general elections, the top-two primary has made campaigns significantly more complex, and some might say more interesting. The reform has also generated frustration due to intra-party races that cause campaign dollars to be spent in so-called “safe” rather than “swing” seats. Of this year’s 25 same-party races, 7 are between Republicans and 18 between Democrats. The result is that Democrats are involved in more intra-party battles than Republicans.
Proposition 14 passed in 55 of 58 counties with a final vote of 53.7% ‘Yes’ to 46.3% ‘No’. Given the facts surrounding the November 2014 election, a strong anecdotal argument can be made that Republican voters supported Proposition 14. The June 2010 election was a high Republican turnout election due to a lively GOP primary gubernatorial contest between Whitman and Poizner, and US senatorial contest between Fiorina, Campbell, and Devore. In fact with an Election Day turnout of 5.6 million, Republicans came within 129,000 voters of Democrat turnout, despite 2.3 million fewer registered Republicans than Democrats in the state.
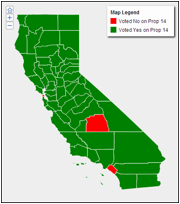The commonly seen pattern of so-called ‘red counties’ voting differently from ‘blue counties’ is not obvious when looking at the election results. Only San Francisco, Orange, and Tulare counties failed to pass the measure. However, further evidence that Republicans likely supported the measure is that in counties where Republican turnout was higher than the Democrat’s the measure passed with 55.6% in favor, nearly 2% higher than the state average.
Although the anecdotal evidence is fairly compelling, it is not dispositive. One could hypothesize that Democrats voted overwhelmingly for the measure, thereby passing Proposition 14 over Republican opposition. To assess this possibility, a more quantitative approach to the data is required. For this analysis I collected the official Proposition 14 turnout and vote totals from the Secretary of State’s website and formulated a least-squares inversion to estimate the level of Republican support using a robust statistical approach.
In the first-order model (found below in the footnote), the inversion that best fits the actual group voting propensities of the 58 counties shows:
- Republicans supported the measure by 52.5% to 47.5%;
- Democrats opposed the measure by a similar margin, 52.2% to 47.8%; and
- Voters registered as neither Republicans or Democrats supported the measure by 69.0% to 31.0%.
Both the anecdotal and quantitative statistical inversion demonstrate that Republicans and unaligned voters both supported the measure by healthy margins.
Honorable Sam Blakeslee, Ph.D. is a former California State Senator and the Founding Director of the Institute for Advanced Technology & Public Policy at California Polytechnic State University, San Luis Obispo.
Footnote:
The problem can be mathematically defined as a minimization of the following equation:
In each of the j different counties, for j=1 to 58, let
A[j,1] = number of ballots cast by registered Republicans and DTS voters who requested a Republican
A[j,2] = number of ballots cast by registered Democrats and DTS voters who requested a Democrat ballot.
A[j,3] = number of ballots cast by everyone else.
Yes[j] = number of yes ballots recorded for Proposition 14
No[j] = number of no ballots recorded for Proposition 14.
Also let the voting propensities for three groups of voters be defined as:
r = probability a voter who voted a Republican ballot voted yes on Proposition 14
d = probability a voter who voted a Democrat ballot voted yes on Proposition 14
o = probability a voter who did not cast a Republican or Democrat ballot voted yes on Proposition 14.
For the sake of simplicity we will ignore those instances in which a voter cast a ballot but skipped voting on Proposition 14. Additionally this analysis assumes that a DTS voter who requested a partisan ballot most likely voted in a manner more consistent with the voting propensities of the members of that party (this assumption was tested and shown to be accurate for this dataset but is not included due to space limitations). For the purposes of this paper these voters are included with the party whose ballot was voted. The probabilities that a voter in each class voted against Proposition 14 are respectively (1-r), (1-d), and (1-o).
Then group voting propensities r, d, and o are found by minimizing the function.